4603. К tilli qraf

n təpəsi, k tili olan qeyri-siklik istiqamətlənmiş qraf verilmişdir. Onun tranzitiv qapanmasındakı tillərin sayını tapmaq lazımdır.

G qrafının tranzitiv qapanması – verilmiş G qrafının təpələrindən və (u, v) tillərindən ibarət olan elə G' qrafıdır ki, ilkin G qrafında həmişə u təpəsindən v təpəsinə yol mövcud olsun.

Knut məsələnin həllini bilir, bəs siz?

Giriş verilənləri. İlk sətirdə n və k (1 ≤ n, k ≤ 50000) ədədləri verilib. Hər sonrakı k sətirdə a_i təpəsi ilə b_i təpəsi arasında tilin mövcudluğunu göstərən iki a_i və b_i tam ədədləri verilir ki, onlar üçün 1 ≤ a_i, b_i ≤ n şərti doğrudur. Qraf dövri deyil, sikl bir neçə təpə ilə eyni vaxtda əlaqələnmiş təpələr mövcud deyil.

Çıxış verilənləri. Tranzitiv qapanmadakı tillərin sayı.

Giriş nümunəsi

5 6

1 2

2 3

3 5

4 5

1 5

1 3

Çıxış nümunəsi

7

Həll

qraflar - maskalar

Alqoritmin analizi

Qrafın təpələrinin alt çoxluğunun maskası olaraq 0 və 1 ədədlərindən ibarət V uzunluqlu ardıcıllığı adlandıracağıq. Maska bitset, və ya tam ədədlər massivində saxlanacaq. Qraf üçün dərinə axtarış alqoritmini işlədəcəyik. Hər bir v təpəsində v-dən əlçatan olan (v-nin özü istisna) təpələr üçün alt çoxluq quracağıq. Əgər v₁, …, v_k (dərinə axtarış alqoritmində) təpələri üçün m₁, …, m_k - övlad maskası olarsa, onda maska aşağıdakı formanı alır:

m₁ or … or m_k or 2^v1 or … or 2^vk

V təpəsindən başlayan tranzitiv qapanmadakı tillərin sayı v-yə uyğun bit maskasında olan 1-lərin sayına bərabərdir.

Nümunə

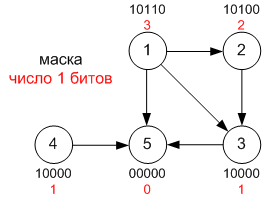
Maskadakı kiçik bit 1 nömrəli təpəyə uyğundur. Bütün maskalardakı bitlərin sayı 3 + 2 + 1 + 1 + 0 = 7 olur. Bu isə, tranzitiv qapanmadakı tillərin sayına bərabərdir.

Alqoritmin həyata keçirilməsi

Qraf üçün uyğun olan bitişik matrisi g massivində saxlayırıq. Dərinə axtarış zamanı keçilmiş təpələri saxlamaq üçün used[] massivindən istifadə edirik. mask[i] massivində isə i təpəsindən əlçatan olan təpələrin bit maskası saxlanır. bits[i] massivi i ədədinin ikili say sistemində yazılışındakı bitlərin sayını saxlayır.

#define MAX 50100

vector <vector<int> > g;

int used[MAX], mask[MAX][MAX/32], bits[1<<16];

V təpəsindən dərinə axtarış alqoritmi.

void dfs(int v)

{

int i, j, to;

used[v] = 1;

for(i = 0; i < g[v].size(); i++)

{

to = g[v][i];

if(!used[to]) dfs(to);

V təpəsinin hər to övladı üçün mask[v] = mask[v] OR mask[to] əmıliyyatını icra edirik.

for(j = 0; j < MaskLen; j++) mask[v][j] |= mask[to][j];

V təpəsinin maskasına to təpəsini əlavə edirik.

mask[v][to >> 5]|= 1 << (to & 31);

}

}

bits massivinin işlənməsi. bits[i] xanası i ədədinin binar formasındakı 1-lərin sayını saxlayır.

int gen(int mask)

{

int i;

if (!mask) return 0;

if (bits[mask]) return bits[mask];

for(i = 0; i < 32; i++)

if (mask & (1 << i)) bits[mask] = gen(mask ^ (1 << i)) + 1;

return bits[mask];

}

Proqramın əsas hissəsi. Daxil olan məlumatı oxuyuruq.

memset(bits,0,sizeof(bits));

gen((1 << 16) - 1);

scanf("%d %d",&n,&k);

g.resize(n);

while(k--)

{

scanf("%d %d",&i,&j);

g[i-1].push_back(j-1);

}

İnt tipli xanada 32 bit saxlanır. Qraf n təpədən ibarətdir. n uzunluqlu maskanı saxlamaq üçün MaskLen = uzunluqlu tam ədəd saxlayan massiv kifayətdir.

MaskLen = (n + 31) / 32;

Dərinə axtarış alqoritmini istifadə edərək hər təpə üçün əlçatanlıq maskası yığılır.

for(i = 0; i < n; i++)

if(!used[i]) dfs(i);

mask[i] maskasında olan 1-ləri sayırıq (0 ≤ i ≤ n – 1).

for(res = 0, i = 0; i < n; i++)

for(j = 0; j < MaskLen ; j++)

res += bits[mask[i][j] & 65535] + bits[(mask[i][j] >> 16) & 65535];

Tranzitiv qapanmadakı tillərin sayını çap edirik.

printf("%d\n", res);

Bitset istifadəsi ilə həll:

#pragma comment (linker, "/STACK:100000000")

#include <cstdio>

#include <vector>

#include <bitset>

#define MAX 50100

using namespace std;

vector <vector<int> > g;

int used[MAX];

int res, n, k, MaskLen;

bitset<MAX> mask[MAX];

void dfs(int v)

{

int i, j, to;

used[v] = 1;

for(i = 0; i < g[v].size(); i++)

{

to = g[v][i];

if(!used[to]) dfs(to);

mask[v] |= mask[to];

mask[v].set(to);

}

}

int main(void)

{

int i, j, r;

scanf("%d %d",&n,&k);

g.resize(n+1);

while(k--)

{

scanf("%d %d",&i,&j);

g[i].push_back(j);

}

for(res = 0, i = 1; i <= n; i++)

{

if(!used[i]) dfs(i);

res += mask[i].count();

}

printf("%d\n", res);

return 0;

}